ジェネラティブ・アートが面白い

久しぶりに Processing でコード書いてます。なんでかと言うと、たまたま本屋さんで見つけた「ジェネラティブ・アート」という本がめちゃくちゃ面白くてそれがきっかけです。

個人的にはChapter 6の「創発」、Chapter 7の「自律性」、Chapter 8の「フラクタル」が特に面白かったです。創発とか自律性の考え方は AI っぽくてゲーム開発にも活かせそうでした。
「ジェネラティブ・アート」は拙著「プロの力を身につける iPhone/iPadアプリケーション開発の教科書」の序章でもプログラミング初心者に最適な本として紹介しています。
プログラミングの楽しさやプロラムが動いたときの感動がダイレクトにわかる良書です。本に掲載されているサンプルプログラムを入力して動かした時に「おお〜」「なるほど！」みたいなわくわくする感じ、ここ最近なかった感覚でした。やっぱり Processing は面白いです。

サンプルプログラムをリファクタリングしてみました

「ジェネラティブ・アート」の最終章「フラクタル」にサトクリフ五角形を作るサンプルがあったのですが、少しプログラムの効率が悪かったので勝手にリファクタリングしてみました。
ちなみにサトクリフ五角形とは数学者であるアラン・サトクリフ氏が考案した五角形です。以下のような五角形のことを指します。

まず五角形を描いて、その 5 つの辺のそれぞれの中点から垂線を引き、この垂 線上の点を結べば別の五角形を作れると言っています。こうすれば、形状の残りの部分も同じ く、さらなる五角形に分けられるので、結局それぞれの五角形がさらに 6 個のサブ五角形に分 けられます。サブ五角形の内にはさらにサブサブ五角形ができるので、この分割を無限小に向 かって繰り返すことができます。

ジェネラティブ・アート 219ページ

再帰的な五角形のコード

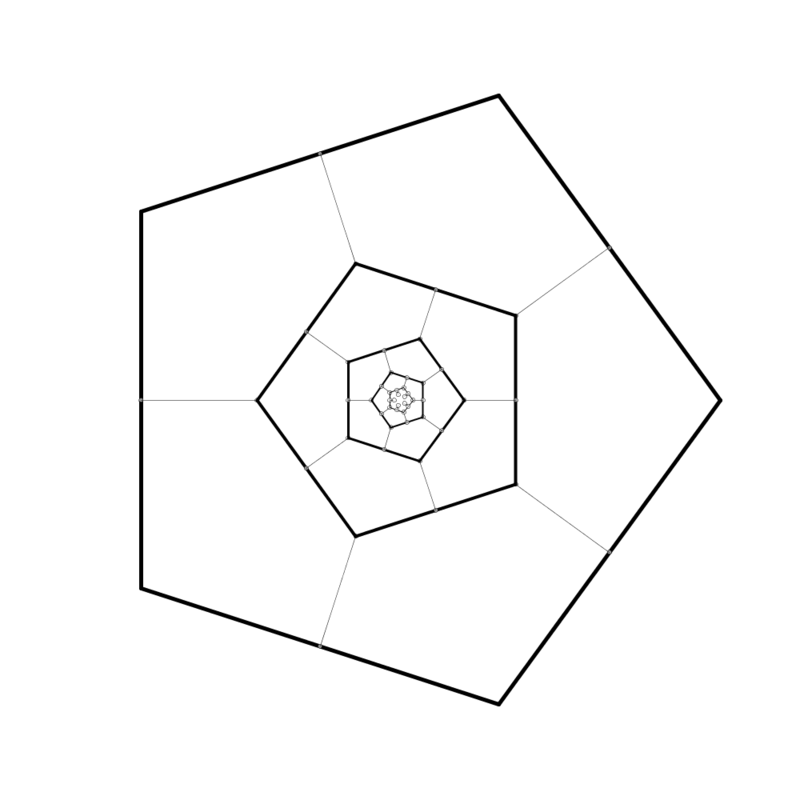
まずは227ページの再帰的な五角形(図8.14)から修正してみます。

FractalRoot pentagon;
int _maxlevels = 5;
float _strutFactor = 0.2;
int _numVertex = 5;

void setup() {
  background(255);
  size(1000, 1000);
  smooth();
  pentagon = new FractalRoot();
  pentagon.drawShape();
}
/*
 * 元のサンプルコードではPointObjという名前でした。
 * クラス名変更しました。
 */
class Point {
  float x, y;
  Point(float ex, float why) {
    x = ex; y = why;
  }
}
/*
 * サンプルコードをそのまま利用する
 */
class FractalRoot {
  Point[] points = new Point[_numVertex];
  Branch rootBranch;
  
  FractalRoot() {
    float centX = width/2;
    float centY = height/2;
    int count = 0;
    for (int i = 0; i < 360; i += 360/_numVertex) {
      float x = centX + (400 * cos(radians(i)));
      float y = centY + (400 * sin(radians(i)));
      points[count] = new Point(x, y);
      count++;
    }
    rootBranch = new Branch(0, 0, points);
  }
  
  void drawShape() {
    rootBranch.drawMe();
  }
}

class Branch {
  int level, num;
  // 頂点
  Point[] vertices;
  
  Branch(int lev, int n, Point[] points) {
    level = lev;
    num =  n;
    vertices = points;
  }
  
  void drawMe() {
    int deg = 0;
    int numVertex = vertices.length;
    Point[] projPoints = new Point[numVertex];
    for (int i = 0; i < numVertex; i++) {
      strokeWeight(5 - level);
      int nexti = i + 1;
      if (nexti == numVertex) {
        nexti = 0;
      }
      // 五角形の一辺を引く
      Point point = vertices[i];
      Point nextPoint = vertices[nexti];
      line(point.x, point.y, nextPoint.x, nextPoint.y);
      // 中点を計算する
      strokeWeight(0.5);
      fill(255, 150);
      Point mid = calcMidPoint(point, nextPoint);
      ellipse(mid.x, mid.y, 5, 5);
      // 中点から垂線を引く
      int destination = i+3;
      if (destination >= numVertex) {
        destination -= numVertex;
      }
      Point proj = calcProjPoint(mid, vertices[destination]);
      line(mid.x, mid.y, proj.x, proj.y);
      ellipse(proj.x, proj.y, 5, 5);
      projPoints[i] = proj;
    }
    
    strokeWeight(0.5);
    fill(255, 150);
    if ((level + 1) < _maxlevels) {
      // 垂線の先から新たに五角形を描く
      Branch childBranch = new Branch(level + 1, 0, projPoints);
      childBranch.drawMe();
    }
  }
  /*
   * サンプルコードをそのまま利用する
   */
  Point calcMidPoint(Point end1, Point end2) {
    :
    : 省略
    :
    return new Point(mx, my);
  }
  Point calcProjPoint(Point mp, Point op) {
    :
    : 省略
    :
    return new Point(px, py);
  }
}

もとのコードは Branch クラスが outerPoints, midPoints, projPoints, myBranches という名前の Point 配列をメンバ変数として保持していました。さすがに配列4つもいらないので1つの配列で管理するように改善しました。
calcMidPoint メソッドと calcProjPoint メソッドの処理は省略しました。処理の中身が気になる方は「ジェネラティブ・アート」を購入して確認してみてください。
出力結果は以下のようになります。

完全なサトクリフ五角形のコード

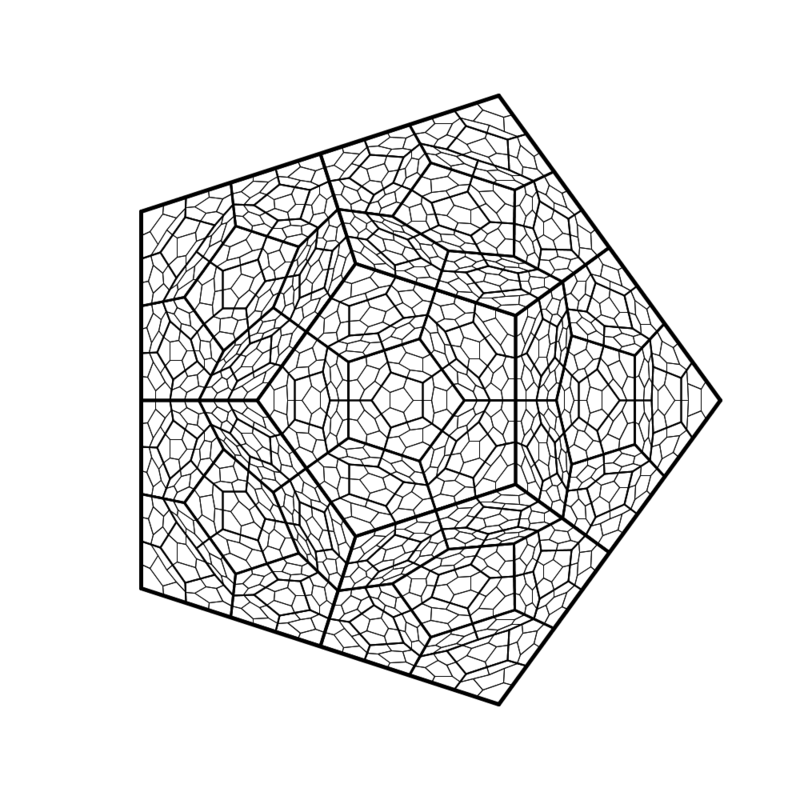
再帰的な五角形のコードをもとに完全なサトクリフ五角形を描画します。修正するのは Branch クラスの drawMe メソッドのみです。

class Branch {
  :
  : 省略
  :
  void drawMe() {
    strokeWeight(5 - level);
    int deg = 0;
    int numVertex = vertices.length;
    Point[] midPoints = new Point[numVertex];
    Point[] projPoints = new Point[numVertex];
    for (int i = 0; i < numVertex; i++) {
      int nexti = i + 1;
      if (nexti == numVertex) {
        nexti = 0;
      }
      // 五角形の一辺を引く
      Point point = vertices[i];
      Point nextPoint = vertices[nexti];
      line(point.x, point.y, nextPoint.x, nextPoint.y);
      Point mid = calcMidPoint(point, nextPoint);
      midPoints[i] = mid;
      int destination = i+3;
      if (destination >= numVertex) {
        destination -= numVertex;
      }
      Point proj = calcProjPoint(mid, vertices[destination]);
      projPoints[i] = proj;
    }
    
    if ((level + 1) < _maxlevels) {
      Branch childBranch = new Branch(level + 1, 0, projPoints);
      childBranch.drawMe();
      for (int i = 0; i < numVertex; i++) {
        int nexti = i-1;
        if (nexti < 0) { nexti += numVertex; }
        Point[] newPoints = { projPoints[i], midPoints[i], vertices[i],
                                  midPoints[nexti], projPoints[nexti] };
        Branch branch = new Branch(level+1, i+1, newPoints);
        branch.drawMe();
      }
    }
  }
  :
  : 省略
  :
}

出力結果は以下のようになります。

参考書籍

• ジェネラティブ・アート